テスラコイルの作り方 (jp)

　テスラコイルのコイル部分の設計方法について, 独自の研究(笑)や調査によって色々分かったのでまとめて紹介します。なお, ココに書いてある方法はあくまで「我流」ですのでそのつもりで^^;

　まずは適当に原理の解説をしますので, 手順だけ知りたければすっ飛ばしても問題は無いでしょう。

テスラコイルにおける最高のコイル

　テスラコイルにおいて, コイルを適当に巻いてしまっては最大のパフォーマンスを得られない事は明白です。ここでいうパフォーマンスとは, 2次回路が完全に共振した場合にトロイド電圧がどれだけ高くできるか, という事とします。同じ共振周波数の2次回路でも, コイルの径や長さ, 容量球の静電容量の組み合わせは無限に存在しますが, その中でも特に放電長を実現できる組み合わせの点を見つけようというものです。最高のコイルを製作すれば, あとは共振周波数をチューニングする作業に集中する事ができ, 最適な共振点を見つけさえすればテスラコイルへの入力電圧に対して最長の放電を得る事が出来ます。テスラコイルは構造だけ見れば簡単に見えますが, 詳しく検証するとなかなか奥が深い代物であります。テスラコイルにおいて2次コイルの電圧を決定する事項はいくつかありますので, それぞれを順に解説していきます。

テスラコイルの構造

テスラコイルの構造は以下のようになっています。

比較的太い電気伝導性の良いワイヤを数回巻いた1次コイルの中に, 細いワイヤを多く巻いた2次コイルが入っている構造をしています。さらに, 2次コイルの下端(1次コイルに近い方)は大地に良質にアースされ, 逆に上方は容量球(トロイド)が接続されます。これは, 実際には放電電極として機能することになります。以下に, 構造だけに注目したテスラコイルの回路図を示します。

構造はこのようにとても簡単ですが, コレをインピーダンスや磁気結合, 寄生容量など電気基礎を諸々考えたマジメな回路(等価回路)で書くと以下のようになります。

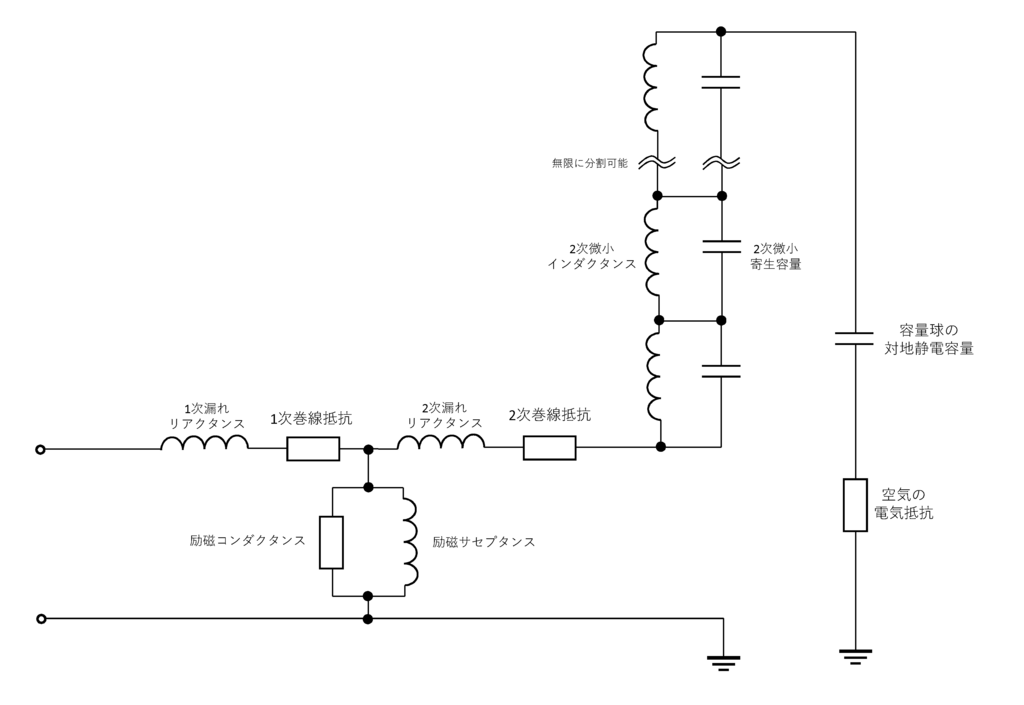
このように多少複雑です。最高のコイルを巻く為に, このような等価回路の回路方程式を計算すれば最適な諸量(インダクタンス, 静電容量等)が算出できますが, とても複雑なうえ, 電気以外の物理事象を全く考慮していないため完璧な結果にはならないでしょう。

とまぁ, テスラコイルの構造はこんなところで。

テスラコイルの放電長を伸ばすには

　せっかくテスラコイルを作るのですから, 放電の長さはできるだけ長くしたいところでしょう。では, テスラコイルにおける放電長をかせぐにはどうすれば良いのか考えます。放電長は電圧の高さによって決まると言っても間違いではありませんが, 放電の様子は環境によって大きく左右される現象です。例えば, 気圧, 温度, 気体の種類, 磁場や電場, 電圧波形など, 多くの物理特性によって大きくその形や長さが変わります。しかし, 標準の場合で説明するためここでは環境は空気で1気圧として話を進める事とします。

　ということで, とにかく電圧を高くすれば放電長が長くなる, という単純な思考で今後は考えます。2次コイルの電圧を高くする方法として, 以下が考えられます。

・1次回路に印加する電圧を高くする

・1次コイルに流れる電流を大きくする

・2次回路の共振をより正確に調整する

・1次回路, 2次回路のQ値をより大きくする

・2次回路の電圧波形の波長を適当になるよう2次コイルを巻く

・結合係数kを適切に調節する

・無駄な放電をしないような構造にする

○1次回路に印加する電圧を高くする

　これは, 変圧器の原理を考えれば分かる事です。1次回路の電圧が高ければ, 自ずと2次側の電圧も比例して高くなります。しかし, 現実的には電源の容量, SGTCの場合はコンデンサの耐圧, SSTC の場合は半導体素子の耐圧&耐流などで制限がかかる事でしょう。

2次コイルの1次コイル近傍は単純な空芯変圧器として見る事ができます。そのため, 1次コイル近傍の2次コイルの巻き数によって, 2次側に誘導される電圧が変化する事になります。この電圧の値は, 2次回路の最終的な出力電圧にとっては重要なファクターです。

○1次コイルに流れる電流を大きくする

　これを達成するために考えられたのがDRSSTCです。1次回路にも共振コンデンサを接続し, 共振させることで1次コイルに大きな電流を流します。その結果, 磁束密度がより高くなり, 2次コイルに誘導される電圧も高くなります。

1次コイルだけの場合, 1次コイルに流れる電流は交流なのでコイルのリアクタンス成分と巻線抵抗により1次コイルに流れる電流は制限されます。しかし, 1次コイルに直列にコンデンサを接続し, この回路を共振周波数で駆動すると1次回路におけるリアクタンス成分は消滅するのと等価になり, よって1次コイルに流れる電流を制限するのは1次コイルの巻線抵抗のみとなります。1次コイルは大抵太く頑丈なワイヤで構成され, 巻き数もそれほど多くないので, おおむね抵抗値は0.5[Ω]以下になると思われますので, 駆動電圧によっては瞬間的に数千[A]ほどの電流を流す事ができます。

○2次回路の共振をより正確に調整する

　正確に共振している程, 2次回路のインピーダンスが最小になり, 容量球-大地間の電圧が最大になります。

○1次回路, 2次回路のQ値をより大きくする

　Q値 (Q factor) は, 共振回路の質を示す値です。RLC直列共振回路では, インダクタンスが大きく, 静電容量と抵抗が小さいほどQ値は大きくなります。つまり, 「できるだけ太いワイヤで, できるだけ径を大きく多く巻く」ことでQ値は大きくする事ができます。1次回路のQ値が高いと, 共振時により大きな電流がコイルを流れ, 2次側により高い電圧が誘導されます。また, 2次回路のQ値が高いと2次回路両端の電圧は高くなります。LC直列共振回路において, コンデンサCの両端には理論上では入力電圧のQ倍の電圧が現れる事になります。

○2次回路の電圧波形の波長を適当になるよう2次コイルを巻く

　電圧が進行する速度は, 銅線内ではほぼ光速であるとされています。2次コイルには高周波交流が流れるので, 容量球の先端が電圧波形における最大部分になるように調整すれば, 容量球部分に現れる電圧は大きくなります。これは電波の発射等で使われるアンテナと同じようなもので, 2次回路の導体長を2次電圧波形の1/4波長となるように2次コイルおよび容量球を設計します。大地アースされてる点で, テスラコイルの2次回路はモノポールアンテナのような物といえます。

上図のように2次コイルをほどいたとした場合, ワイヤ長+容量球までの導体長+アース導体長から決まる2次回路長が駆動周波数の1/4波長の場合とそうでない場合とでは, 容量球部の対地電圧が変わってくるのが分かると思います。つまり, 2次コイルの設計で重要なのは, 共振周波数の波長とワイヤ長を可能な限り一致させる事です。

○結合係数kを適切に調節する

　2次側が共振するにあたり, 電圧の自由振動を妨げるほど1次コイルと2次コイルの結合を強くしすぎてはいけません。まぁ, 大抵のテスラコイルは空芯コイルとなるはずなので, せいぜい高くて k = 0.1~0.3 ほどでしょう。私の実験によれば, 結合係数は k = 0.25程がベストでした。結合係数は, コイルの形状と2コイル間の距離, 環境の透磁率によって決まる係数です。

○無駄な放電をしないような構造にする

　容量球以外の箇所で起こる放電は完全に無駄な物で損失になります。これを防ぐには, コイルの構造をしっかりと考えなければなりません。例えば, 1次コイルと2次コイルの間で放電しないように十分な距離をとったり, 1次コイルをフラットコイルにする, などです。

最高のコイルの設計方法

　以上の事項を踏まえてコイルを設計すれば, それは最高のコイルといえるでしょう。しかし, これらの条件を全てバランス良く満たしたコイルを設計するのはそう簡単ではありません。それでは, 実際にどのように2次コイルを設計すれば良いのかを解説します。

　「テスラコイルの放電を伸ばすには」に示した条件から, 共振周波数, インダクタンス, 電圧の伝播速度やワイヤの静電容量, Q値の計算式等から諸量の関係式を求め, また実験で得られた結果や既存の論文から得られたデータを用いて関係を具体化した結果, 以下の式が導かれました。「Kamomesanの公式」とでも呼びましょうかね(笑)

N は2次コイルの巻き数です。この式がすばらしいのは, テスラコイルを作るにあたって, 使用するマグネットワイヤの直径 w, 容量球の容量 C が分かるだけで, 上記「テスラコイルの放電長を伸ばすには」で説明した条件のほとんどをクリアしたコイルが巻けるという事にあります。さらに, ワイヤ径と容量球容量は自分の好みで簡単に設定できる値ですね。kamomesanの公式で求められた回数だけ2次コイルを巻けば良いので, あとは測定により共振周波数をもとめ, その共振周波数にあわせた1次回路を作成するだけです。kamomesanの公式では, 最適な容量球の静電容量と巻き数の関係が分かりますので, その関係をできるだけQ値が高くなるようにフィルタリングする事で, 最高のコイルを設計できます。RLC直列共振回路のQ値は次式で算出できます。

ここで, 巻線抵抗 R は銅の抵抗率と巻き数から, 次式で求められます。

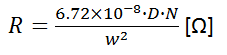
インダクタンス L を計算するにあたり長岡係数 A が必要になりますが, 長岡係数の計算は非常に複雑なので, 以下に示すコイルの径長比 a と独自に算出した長岡係数の近似式を用いて計算します。

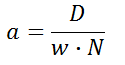
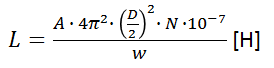
算出された巻線抵抗 R, インダクタンス L と, 容量球の静電容量 C を Q値の式に代入する事でQ値が計算できます。kamomesanの公式とQ値の算出式を用いることで, 以下のグラフのように容量球の静電容量を変数とした時の共振周波数, Q値, 巻き数 の関係を計算する事が出来ます。

ワイヤ径は0.3[mm]のものを, VU65 (塩ビパイプ) に巻いた時の諸量の関係です。実際に製作できる1次回路の周波数にはスイッチング素子等の応答速度により限界があります。ここで, 仮に製作できる1次回路の最高発振周波数を500[kHz]とすると, 上グラフより, 巻き数はおよそ 626 [回], 容量球の容量は 10 [pF], Q値は 894 であると求める事ができます。この値どおりに2次コイルを巻いた時, そのコイルは「テスラコイルの放電を伸ばすには」に示した条件を満たした物とするとができます。グラフを見れば分かりますが, 1次回路で発振できる周波数が高ければ高いほど, また1次回路の電圧が高ければ高いほど, チューニングはシビアになりますがQ値が大きくなるので大きな放電を期待できることになります。

　2次コイルが設計できたら次に1次コイルです。上で作成した2次回路の下部に適当な1次コイルモドキを巻き, 小信号の矩形波を入力する事で, オシロスコープを使用して2次回路の共振周波数を測定します。下図のように装置をセッティングし, 周波数可変の小信号矩形波源(正弦波でも可)の周波数を調整して, オシロスコープに表示される波形の振幅が最大になる周波数(共振周波数)を見つけます。この時注意すべきなのが, 測定の誤差になるので容量球に手などを近づけすぎないという事と, プローブを容量球に近づけすぎない事です。スパークがプローブに当たると最悪オシロスコープが壊れてしまいます^^; 容量球とプローブの距離で波形が大分変化するので, プローブは何らかの方法で固定するのが楽でしょう。

オシロスコープが無い場合は, LCRメータで直接インダクタンスを測定して共振周波数を推測する方法もありますが, この場合では容量球の静電容量の測定が難しく, うまく共振周波数を求められないでしょう。テスラコイルをやるならオシロスコープは1台くらい持っておいた方が良いと思います。今後の電子工作でも必ず使うときが来ますので^^

　後は簡単で, 測定した2次側共振周波数で共振するような1次回路を設計するだけです。このときの注意は,

○ 1次コイルに使うワイヤは出来るだけ太く, 銅などの電気伝導性の良い素材を使う。

○ できるだけコイルの巻き数を多くする。

○ 1次-2次コイル間での放電を防ぐため, 2次コイルとはある程度離す。1次コイルと2次コイルの間にどれだけ電位差が出来る(放電しやすい)かは, アース線の長さや1次コイルの形状によって左右されるので, テスラコイルの規模にもよりますが最低でも10mmは離した方が良いかも知れません。

○ 逆コーン状のコイルはお勧めしません。電磁気的にはあの形状にするメリットは得に無いです。

くらいでしょうか。とにかく, 1次コイルが燃えないように, また2次コイル間とで放電しないようにすれば問題無いでしょう。

最終的なテスラコイルの設計手順

　導かれた関係式を用いる事で簡単にテスラコイルに最適な2次コイルを設計する事が出来ます。手順は大体以下のようになるでしょう。

① 作りたいテスラコイルのサイズを大まかに決める。

② 2次コイルを巻く空芯筒(塩ビパイプ等)の直径を決める。

③ テスラコイルのサイズを気にして, 2次コイルに使うマグネットワイヤーの径 w を決定する。(後の検証でコイル径に対する理想的なワイヤ径が分かったりします。)

④ 外部のサイトを利用するなどして, 容量球のサイズと大体の静電容量 C を決定する。

⑤ kamomesanの公式に決定した値 w, C を代入して2次コイルの巻き数 N を得る。

⑥ 決めたサイズの容量球を作れる分の材料, 2次コイル用のマグネットワイヤーを購入する。

⑦ 2次コイルを決めた巻き数だけ巻き, 容量球も設計通りに製作する。

⑧ 2次コイルと容量球を合体し, 適当な1次コイルを巻いて共振周波数を測定する。

⑨ 測定した2次コイルの共振周波数と共振するように, かつ燃えないように, 2次コイル間でスパークしないよう気を付けて1次回路を組む。

⑩ 容量球を納得いくまで微調節する。

⑪ やったぜ。

kamomesanの公式を簡単に計算できるExcelシートを用意したので, よければ使ってください。↓

TeslaCoil_calclation_form.xlsx - Google ドライブ

 kamomesanの公式の検証

　導かれたkamomesanの公式を用いて, 実際にいくつか事例を設定し, 最適なコイルはどのような物になるのかを計算してみたいと思います。

○ [問1] 最高周波数 500 [kHz] の1次フルブリッジ回路を設計できるA氏がいる。手元にVU250のパイプとφ0.4[mm]のUEWがあるとし, 放電長が最大になる為にはA氏は2次コイルを何回巻けば良いか, およびトロイドの容量はいくつにすれば良いかを求めよ。

ここで, UV250は直径が 267[mm], マグネットワイヤの直径が 0.4[mm] と分かっているので, コイル径 D は 267.4[mm], ワイヤ径 w は 0.4[mm] となります。これらの値をkamomesanの公式に代入し, さらにQ値を計算すると以下のグラフに表す特性が求められます。

このグラフから, A氏が作る1次回路の 500 [kHz] で最長の放電を得るためには, 2次コイルの巻き数は 1400 [回], トロイドの静電容量は 30 [pF] と求まります。ちなみに, Q値は 523 です。よって, A氏が作るべき2次コイルは以下のようになるでしょう。

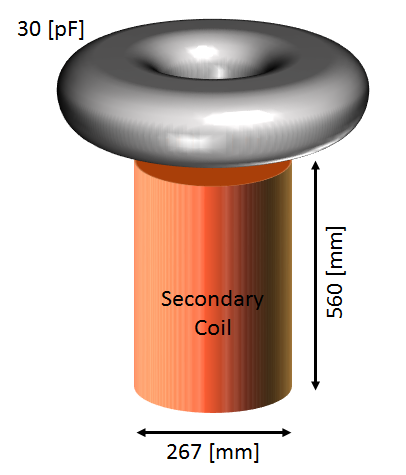
実際には, コイルが短いことにより放電が下に接触してしまうと思われるので, ここから構造的に放電長を伸ばす工夫をする事になると思います。トロイドを高い位置に持っていったり, コイルを巻くパイプ内に絶縁物を詰め込んだり, 設置抵抗を小さくしたり, こだわるならマグネットワイヤーを太いものに変えて巻きなおすのも良いでしょう^^。

○ [問2] 手元にVU65にφ0.1[mm]のUEWを1500[回]巻いた2次コイルを持っているB氏がいる。放電長が最大になる為には, B氏は何pFのトロイドを用意し, 1次回路の発振周波数を何[kHz]にすれば良いかを求めよ。

VU65 の直径は 76[mm]で, マグネットワイヤーの直径が 0.1[mm] と分かっているので, コイル径 D = 76.1[mm], w = 0.1[mm] です。これをkamomesanの公式に代入し, それによって得られた関係からQ値を計算すると以下のグラフに示すような特性が得られます。

このグラフから, 放電を最長にするのに必要なトロイドの静電容量は 16 [pF], この時の共振周波数は 202.6 [kHz] であると求められます。ちなみにQ値は 256 です。

○ [問3] 最高周波数 600 [kHz] の1次フルブリッジ回路を設計できるC氏がいる。手元にVU600のパイプとφ0.6[mm]のUEWがあるとし, 放電長が最大になる為にはC氏は2次コイルを何回巻けば良いか, およびトロイドの容量はいくつにすれば良いか, 1次回路の発振周波数は何kHzにすれば良いかを求めよ。

ここで, UV600は直径が 632[mm], マグネットワイヤの直径が 0.6[mm] と分かっているので, コイル径 D は 632.6[mm], ワイヤ径 w は 0.6[mm] となります。これらの値をkamomesanの公式に代入し, さらにQ値を計算すると以下のグラフに表す特性が求められます。

このグラフから, 最長の放電を得るためには, 2次コイルの巻き数は 252 [回], トロイドの静電容量は 8 [pF] , 1次回路の発振周波数は 252 [kHz] と求まります。ちなみに, Q値は 2660 です。このコイルでは, 巻き数とワイヤ径から分かるように高さが 151 [mm] と, 太く短いコイルになっていることが分かります。この形状は, 放電長を稼ぐのには不向きですので, 実際には多少Q値をあきらめてワイヤ径をさらに大きい物で巻きなおす事や, トロイドを大きなものにする改善が必要となるでしょう。大きいコイルで迫力を求めるほど, 大きなトロイドと太い巻線が必要な事がわかります。

実際に実験してみる

準備中